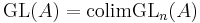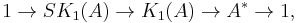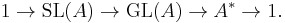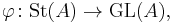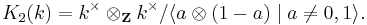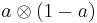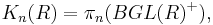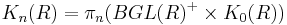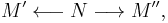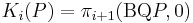Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequence
- Kn(R)
of functors from rings to abelian groups, for all integers n. For historical reasons, the lower K-groups K0 and K1 are thought of in somewhat different terms from the higher algebraic K-groups Kn for n ≥ 2. Indeed, the lower groups are more accessible, and have more applications, than the higher groups. The theory of the higher K-groups is noticeably deeper, and certainly much harder to compute (even when R is the ring of integers).
The group K0(R) generalises the construction of the ideal class group of a ring, using projective modules. Its development in the 1960s and 1970s was linked to attempts to solve a conjecture of Serre on projective modules that now is the Quillen-Suslin theorem; numerous other connections with classical algebraic problems were found in this era. Similarly, K1(R) is a modification of the group of units in a ring, using elementary matrix theory. The group K1(R) is important in topology, especially when R is a group ring, because its quotient the Whitehead group contains the Whitehead torsion used to study problems in simple homotopy theory and surgery theory; the group K0(R) also contains other invariants such as the finiteness invariant. Since the 1980s, algebraic K-theory has increasingly had applications to algebraic geometry. For example, motivic cohomology is closely related to algebraic K-theory.
Contents |
History
Alexander Grothendieck discovered K-theory in the mid-1950s as a framework to state his far-reaching generalization of the Riemann-Roch theorem. Within a few years, its topological counterpart was considered by Michael Atiyah and Hirzebruch and is now known as topological K-theory.
Applications of K-groups were found from 1960 onwards in surgery theory for manifolds, in particular; and numerous other connections with classical algebraic problems were brought out.
A little later a branch of the theory for operator algebras was fruitfully developed, resulting in operator K-theory and KK-theory. It also became clear that K-theory could play a role in algebraic cycle theory in algebraic geometry (Gersten's conjecture): here the higher K-groups become connected with the higher codimension phenomena, which are exactly those that are harder to access. The problem was that the definitions were lacking (or, too many and not obviously consistent). Using work of Robert Steinberg on universal central extensions of classical algebraic groups, John Milnor defined the group K2(A) of a ring A as the center, isomorphic to H2(E(A),Z), of the universal central extension of the group E(A) of infinite elementary matrices over A. (Definitions below.) There is a natural bilinear pairing from K1(A) × K1(A) to K2(A). In the special case of a field k, with K1(k) isomorphic to the multiplicative group GL(1,k), computations of Hideya Matsumoto showed that K2(k) is isomorphic to the group generated by K1(A) × K1(A) modulo an easily described set of relations.
Eventually the foundational difficulties were resolved (leaving a deep and difficult theory) by Quillen (1973, 1974), who gave several definitions of Kn(A) for arbitrary non-negative n, via the +-construction and the Q-construction.
Lower K-groups
The lower K-groups were discovered first, and given various ad hoc descriptions, which remain useful. Throughout, let A be a ring.
K0
The functor K0 takes a ring A to the Grothendieck group of the set of isomorphism classes of its finitely generated projective modules, regarded as a monoid under direct sum. Any ring homomorphism A → B gives a map K0(A) → K0(B) by mapping (the class of) a projective A-module M to M⊗AB, making K0 a covariant functor.
If the ring A is commutative, we can define a subgroup 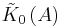 of K0(A) as the set
of K0(A) as the set 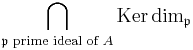 , where
, where 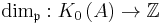 is the map sending every (class of a) finitely generated projective A-module M to the rank of the free
is the map sending every (class of a) finitely generated projective A-module M to the rank of the free 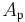 -module
-module 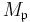 (this module is indeed free, as any finitely generated projective module over a local ring is free). This subgroup
(this module is indeed free, as any finitely generated projective module over a local ring is free). This subgroup 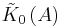 is known as the reduced zeroth K-theory of A.
is known as the reduced zeroth K-theory of A.
Examples: (Projective) modules over a field k are vector spaces and K0(k) is isomorphic to Z, by dimension. For A a Dedekind ring,
- K0(A) = Pic(A) ⊕ Z,
where Pic(A) is the Picard group of A, and similarly the reduced K-theory is given by
An algebro-geometric variant of this construction is applied to the category of algebraic varieties; it associates with a given algebraic variety X the Grothendieck's K-group of the category of locally free sheaves (or coherent sheaves) on X. Given a compact topological space X, the topological K-theory Ktop(X) of (real) vector bundles over X coincides with K0 of the ring of continuous real-valued functions on X. [1]
K1
Hyman Bass provided this definition, which generalizes the group of units of a ring: K1(A) is the abelianization of the infinite general linear group:
Here
is the direct limit of the GLn, which embeds in GLn+1 as the upper left block matrix, and the commutator subgroup agrees with the group generated by elementary matrices ![\operatorname{E}(A)=[\operatorname{GL}(A),\operatorname{GL}(A)]](/2012-wikipedia_en_all_nopic_01_2012/I/fa65e30f09e43aeea20f4043115c57ea.png) , by Whitehead's lemma. Indeed, the group
, by Whitehead's lemma. Indeed, the group 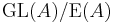 was first defined and studied by Whitehead,[2] and is called the Whitehead group of the ring A.
was first defined and studied by Whitehead,[2] and is called the Whitehead group of the ring A.
Commutative rings and fields
For A a commutative ring, one can define a determinant 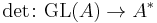 to the group of units of A, which vanishes on
to the group of units of A, which vanishes on 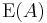 and thus descends to a map
and thus descends to a map 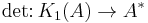 . As
. As 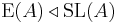 , one can also define the special Whitehead group
, one can also define the special Whitehead group 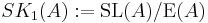 . This map splits via the map
. This map splits via the map 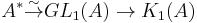 (unit in the upper left corner), and hence is onto, and has the special Whitehead group as kernel, yielding the split short exact sequence:
(unit in the upper left corner), and hence is onto, and has the special Whitehead group as kernel, yielding the split short exact sequence:
which is a quotient of the usual split short exact sequence defining the special linear group, namely
Thus, since the groups in question are abelian, 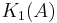 splits as the direct sum of the group of units and the special Whitehead group:
splits as the direct sum of the group of units and the special Whitehead group: 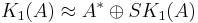 .
.
When A is a Euclidean domain (e.g. a field, or the integers) SK1(A) vanishes, and the determinant map is an isomorphism. In particular, 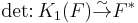 . This is false in general for PIDs, thus providing one of the rare mathematical features of Euclidean domains that do not generalize to all PIDs. An explicit PID A such that SK1(A) is nonzero was given by Grayson in 1981. If A is a Dedekind domain whose quotient field is a finite extension of the rationals then Milnor (1971, corollary 16.3) shows that SK1(A) vanishes.
. This is false in general for PIDs, thus providing one of the rare mathematical features of Euclidean domains that do not generalize to all PIDs. An explicit PID A such that SK1(A) is nonzero was given by Grayson in 1981. If A is a Dedekind domain whose quotient field is a finite extension of the rationals then Milnor (1971, corollary 16.3) shows that SK1(A) vanishes.
For a non-commutative ring, the determinant cannot be defined, but the map 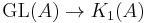 generalizes the determinant.
generalizes the determinant.
K2
John Milnor found the right definition of K2 for fields: it is the center of the Steinberg group 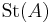 of A.
of A.
It can also be defined as the kernel of the map
or as the Schur multiplier of the group of elementary matrices.
Matsumoto's theorem says that for a field k, the second K-group is given by[3]
Matsumoto's original theorem is even more general: For any root system, it gives a presentation for the unstable K-theory. This presentation is different from the one given here only for symplectic root systems. For non-symplectic root systems, the unstable second K-group with respect to the root system is exactly the stable K-group for 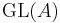 . Unstable second K-groups (in this context) are defined by taking the kernel of the universal central extension of the Chevalley group of universal type for a given root system. This construction yields the kernel of the Steinberg extension for the root systems
. Unstable second K-groups (in this context) are defined by taking the kernel of the universal central extension of the Chevalley group of universal type for a given root system. This construction yields the kernel of the Steinberg extension for the root systems 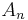 (
(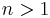 ) and, in the limit, stable second K-groups.
) and, in the limit, stable second K-groups.
Milnor K-theory
The above expression for K2 of a field k led Milnor to the following definition of "higher" K-groups by
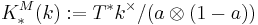 ,
,
thus as graded parts of a quotient of the tensor algebra of the multiplicative group k× by the two-sided ideal, generated by the
for a ≠ 0,1. For n = 0,1,2 these coincide with those below, but for n≧3 they differ in general.[4] For example, we have 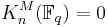 for n≧3. Milnor K-theory modulo 2 is related to étale (or Galois) cohomology of the field by the Milnor conjecture, proven by Voevodsky.[5] The analogous statement for odd primes is the Bloch-Kato conjecture, proved by Voevodsky, Rost, and others.
for n≧3. Milnor K-theory modulo 2 is related to étale (or Galois) cohomology of the field by the Milnor conjecture, proven by Voevodsky.[5] The analogous statement for odd primes is the Bloch-Kato conjecture, proved by Voevodsky, Rost, and others.
Higher K-theory
The definitive definitions of higher K-groups were given by Quillen (1973), after a few years during which several incompatible definitions were suggested.
The +-construction
One possible definition of higher algebraic K-theory of rings was given by Quillen
Here 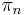 is a homotopy group, GL(R) is the direct limit of the general linear groups over R for the size of the matrix tending to infinity, B is the classifying space construction of homotopy theory, and the + is Quillen's plus construction.
is a homotopy group, GL(R) is the direct limit of the general linear groups over R for the size of the matrix tending to infinity, B is the classifying space construction of homotopy theory, and the + is Quillen's plus construction.
This definition only holds for n>0 so one often defines the higher algebraic K-theory via
Since BGL(R)+ is path connected and K0(R) discrete, this definition doesn't differ in higher degrees and also holds for n=0.
The Q-construction
The Q-construction gives the same results as the +-construction, but it applies in more general situations. Moreover, the definition is more direct in the sense that the K-groups, defined via the Q-construction are functorial by definition. This fact is not automatic in the +-construction.
Suppose P is an exact category; associated to P a new category QP is defined, objects of which are those of P and morphisms from M′ to M″ are isomorphism classes of diagrams
where the first arrow is an admissible epimorphism and the second arrow is an admissible monomorphism.
The i-th K-group of P is then defined as
with a fixed zero-object 0, where BQ is the classifying space of Q, which is defined to be the geometric realisation of the nerve of Q.
This definition coincides with the above definitions of K0.
The K-groups 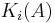 of the ring A are then the K-groups
of the ring A are then the K-groups 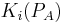 where
where 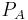 is the category of finitely generated projective A-modules. More generally, for a scheme X, the higher K-groups of X are by definition the K-groups of (the exact category of) locally free coherent sheaves on X.
is the category of finitely generated projective A-modules. More generally, for a scheme X, the higher K-groups of X are by definition the K-groups of (the exact category of) locally free coherent sheaves on X.
The following variant of this is also used: instead of finitely generated projective (=locally free) modules, take finitely generated modules. The resulting K-groups are usually called G-groups, or higher G-theory. When A is a noetherian regular ring, then G- and K-theory coincide. Indeed, the global dimension of regular local rings is finite, i.e. any finitely generated module has a finite projective resolution, so the canonical map K0 → G0 is surjective. It is also injective, as can be shown. This isomorphism extends to the higher K-groups, too.
The S-construction
A third construction of K-theory groups is the S-construction, due to Waldhausen.[6] It applies to categories with cofibrations (also called Waldhausen categories). This is a more general concept than exact categories.
Examples
While the Quillen algebraic K-theory has provided deep insight into various aspects of algebraic geometry and topology, the K-groups have proved particularly difficult to compute except in a few isolated but interesting cases.
Algebraic K-groups of finite fields
The first and one of the most important calculations of the higher algebraic K-groups of a ring were made by Quillen himself for the case of finite fields:
If Fq is the finite field with q elements, then
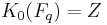 ,
, 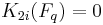
for 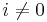 , and
, and
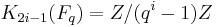 for i≥1.
for i≥1.
Algebraic K-groups of rings of integers
Quillen proved that if A is the ring of algebraic integers in an algebraic number field F (a finite extension of the rationals), then the algebraic K-groups of A are finitely generated. Borel used this to calculate Ki(A) and Ki(F) modulo torsion. For example, for the integers Z, Borel proved that (modulo torsion)
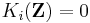 for positive i unless
for positive i unless 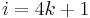 with k positive
with k positive
and (modulo torsion)
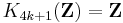 for positive k.
for positive k.
The torsion subgroups of K2i+1(Z), and the orders of the finite groups K4k+2(Z) have recently been determined, but whether the latter groups are cyclic, and whether the groups K4k(Z) vanish depends upon Vandiver's conjecture about the class groups of cyclotomic integers. See Quillen-Lichtenbaum conjecture for more details.
Applications and open questions
Algebraic  -groups are used in conjectures on special values of L-functions and the formulation of an non-commutative main conjecture of Iwasawa theory and in construction of higher regulators.
-groups are used in conjectures on special values of L-functions and the formulation of an non-commutative main conjecture of Iwasawa theory and in construction of higher regulators.
Another fundamental conjecture due to Hyman Bass (Bass conjecture) says that all G-groups G(A) (that is to say, K-groups of the category of finitely generated A-modules) are finitely generated when A is a finitely generated Z-algebra.[7]
References
- ^ Karoubi, Max (2008), K-Theory: an Introduction, Classics in mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-79889-7, see Theorem I.6.18
- ^ J.H.C. Whitehead, Simple homotopy types Amer. J. Math. , 72 (1950) pp. 1–57
- ^ Matsumoto, Hideya (1969), "Sur les sous-groupes arithmétiques des groupes semi-simples déployés", Ann. Sci. École Norm. Sup. 4 (2): 1–62, MR0240214, http://www.numdam.org/item?id=ASENS_1969_4_2_1_1_0
- ^ (Weibel 2005), cf. Lemma 1.8
- ^ Voevodsky, Vladimir (2003), "Motivic cohomology with Z/2-coefficients", Institut des Hautes Études Scientifiques. Publications Mathématiques 98 (98): 59–104, doi:10.1007/s10240-003-0010-6, ISSN 0073-8301, MR2031199
- ^ Waldhausen, Friedhelm (1985), "Algebraic K-theory of spaces", Algebraic K-theory of spaces, Lecture Notes in Mathematics, 1126, Berlin, New York: Springer-Verlag, pp. 318–419, doi:10.1007/BFb0074449, ISBN 978-3-540-15235-4, MR802796. See also Lecture IV and the references in (Friedlander & Weibel 1999)
- ^ (Friedlander & Weibel 1999), Lecture VI
- Friedlander, Eric; Grayson, Daniel, eds. (2005), Handbook of K-Theory, Berlin, New York: Springer-Verlag, ISBN 978-3-540-30436-4, MR2182598, http://www.springerlink.com/content/978-3-540-23019-9/
- Friedlander, Eric M.; Weibel, Charles W. (1999), An overview of algebraic K-theory, World Sci. Publ., River Edge, NJ, pp. 1–119, MR1715873
- Milnor, John Willard (1969 1970), "Algebraic K-theory and quadratic forms", Inventiones Mathematicae 9 (4): 318–344, doi:10.1007/BF01425486, ISSN 0020-9910, MR0260844
- Milnor, John Willard (1971), Introduction to algebraic K-theory, Princeton, NJ: Princeton University Press, MR0349811 (lower K-groups)
- Quillen, Daniel (1973), "Higher algebraic K-theory. I", Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), Lecture Notes in Math, 341, Berlin, New York: Springer-Verlag, pp. 85–147, doi:10.1007/BFb0067053, ISBN 978-3-540-06434-3, MR0338129
- Quillen, Daniel (1975), "Higher algebraic K-theory", Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), Vol. 1, Montreal, Quebec: Canad. Math. Congress, pp. 171–176, MR0422392 (Quillen's Q-construction)
- Quillen, Daniel (1974), "Higher K-theory for categories with exact sequences", New developments in topology (Proc. Sympos. Algebraic Topology, Oxford, 1972), London Math. Soc. Lecture Note Ser., 11, Cambridge University Press, pp. 95–103, MR0335604 (relation of Q-construction to +-construction)
- Rosenberg, Jonathan (1994), Algebraic K-theory and its applications, Graduate Texts in Mathematics, 147, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94248-3, MR[http://www-users.math.umd.edu/~jmr/KThy_errata2.pdf Errata 1282290 [http://www-users.math.umd.edu/~jmr/KThy_errata2.pdf Errata]], http://books.google.com/books?id=TtMkTEZbYoYC
- Seiler, Wolfgang (1988), "λ-Rings and Adams Operations in Algebraic K-Theory", in Rapoport, M.; Schneider, P.; Schappacher, N., Beilinson's Conjectures on Special Values of L-Functions, Boston, MA: Academic Press, ISBN 978-0-12-581120-0
- Weibel, Charles (2005), "Algebraic K-theory of rings of integers in local and global fields", Handbook of K-theory, Berlin, New York: Springer-Verlag, pp. 139–190, MR2181823, http://www.math.uiuc.edu/K-theory/0691/KZsurvey.pdf (survey article)
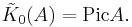
![K_1(A) = \operatorname{GL}(A)^{\mbox{ab}} = \operatorname{GL}(A) / [\operatorname{GL}(A),\operatorname{GL}(A)]](/2012-wikipedia_en_all_nopic_01_2012/I/4d76bfdb6434b97968c7a7b0a65fcbce.png)